I Have Words! Give Me Sentences! - Sentence Embeddings

30 Jun 2018

Word embeddings are the staple of any Natural Language Processing (NLP) task. In fact, representation of words in the form of vectors is probably the first step in building any NLP application. These vector representations of words fall in a wide spectrum in semantic encoding space, with a one-hot representation on one end of the spectrum, encoding absolutely nothing in terms of semantics between words and the other end of the spectrum still being an active area of research with ELMo embeddings achieving state of the art results. Most widely used embeddings such as Word2Vec and GloVe fall somewhere in between on this spectrum.

Although these word embeddings encode semantic relationships between words and can be efficiently used as vector representations of words, these embeddings cannot directly be applied to NLP tasks. Majority of NLP tasks deal in sentences and paragraphs (a set of words, to be more formal) and not individual words themselves. Therefore, there is a need for efficient semantic embeddings for groups of words, henceforth referred to as sentence embeddings.

Averaging of individual Word2Vec embeddings is one of the most widely used sentence embedding techniques. Although it might sound naive, hey, it works. There definitely exists some information loss when we average out word2vec vectors which get cancelled out when another learning algorithm is stacked after the averaging operation.

Another approach to sentence embedding is to treat the words in a sentence as sequence inputs at respective time steps. Hence, it can be modeled using a recurrent neural network architecture where the each word is treated as input at current time step. The encoded representation or the last hidden state activation at the final time step is taken as the sentence embedding.

One of the most recent research in sentence encoding comes from Google, which has open sourced their implementation in the form of Universal Sentence Encoder. Universal Sentence Encoder is an implementation of two sentence encoding architectures, Deep Averaged Networks and Transformer.

Deep Averaged Network is a simple feed forward neural network that takes the average of word embeddings as the input layer, stacks two hidden layers and culminates with a softmax over the target classification. The last hidden layer activation is taken as the sentence embedding.

The Transformer architecture is a variant of recurrent neural network, where a convolution is implemented over the input sentence. Each word is embedded using an existing word embedding technique with an additional positional embedding. These word embeddings are passed through a convolutional layer with attention mechanism. The decoder stage generates the context/future words given a sequence of words. The hidden state activation is taken as the sentence embedding.

While these approaches are promising, employing complex neural architectures fail to perform significantly better than simple old-fashioned averaging of word vectors. In most of the NLP tasks, instead of employing such complicated architectures in your model, you will be better off employing simple average based sentence encodings and optimizing your classification model.

Since we have decided to go down the averaging route, we can explore different kinds of averaging in order to better embed sentences. One of the approaches is to employ tf-idf weighted average of word vectors instead of a simple average, which in practice turns out to be an embarrassingly good sentence embedding. Any averaging technique is dependent on the quality of the underlying word embeddings. Therefore, any improvement in word embeddings has a direct effect on sentence embeddings. This is where ELMo embeddings come into the picture.

ELMo (Em-beddings from Language Models) is a word representation algorithm that is providing state of the art results in downstream NLP tasks. They are presented in the following paper: Deep Contextualized Word Representations. The architecture consists of 1 word embedding layer and 2 hidden bi-LSTM layers, for both forward and backward representations. ELMo is modeled on image classification neural network ResNet and hence, the defining characteristic of ELMo is that it exposes the hidden layer activations for each word. A weighted average of these activations yield the word embedding. These weights are learnable parameters and can be fine tuned for the NLP task at hand. Since the entire ELMo model is pre trained on big corpus and only these weights are learned for the task at hand, it falls into transfer learning territory and is best suited for any NLP task with less amount of data.

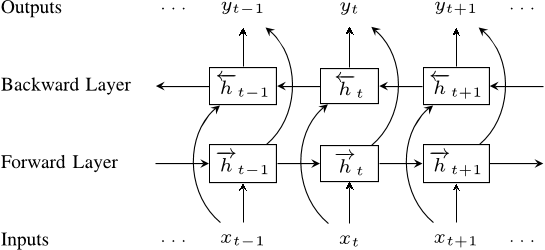
One important point about the above architecture is that, ELMo takes words as input character wise. A 2048 character n gram convolutional filter is applied on the characters of the words, followed by a projection on the 512 dimension vector space for each word. This gives ELMo the ability to handle unseen words and even commonly miss-spelt words.

Assume that ( t_{k} ) is the current word (token) that needs to be embedded, the following probabilities is modeled by the forward and backward LSTM layers:

\[p(t_{1},t_{2},...,t_{N}) = \prod_{k=1}^{N}p(t_{k}|t_{1},t_{2},...,t_{k-1})\] \[p(t_{1},t_{2},...,t_{N}) = \prod_{k=1}^{N}p(t_{k}|t_{k+1},t_{k+2},...,t_{N})\]

Given the token ( t_{k} ) (word), the convolutional filter is applied on the characters and projected into the word embedding space. This projection is denoted by ( x_{k} ).

If the architecture consists of ( L ) hidden layers, for the token ( t_{k} ), we get ( 2L ) hidden representations (forward and backward) and 1 word embedding representation ( x_{k} ), which can be represented as:

\[R_{k} = \{x_{k}, h_{k,j}^{forward}, h_{k,j}^{backward} | j=1,2,...,N\}\]

Concatenating the forward and backward representations, each token ( t_{k} ) has ( 2L+1 ) representations, which can expressed as:

\[R_{k} = \{h_{k,j} | j=0,1,2,...,N\}, where \quad h_{0,j}=x_{k}\]

Now, the ELMo representation of this word (which is task dependent) is expressed as:

\[ELMo_{k}^{task} = \gamma^{task}\sum_{j=0}^{L}s_{j}^{task}h_{k,j}\]

where \(\gamma^{task}\) is a scaling parameter.

Both \(\gamma^{task}\) and \(s_{j}^{task}\) are learnable parameters that are trained specific to the NLP task at hand.