Interpreting Machine Learning Models - Part 5
16 Sep 2019Link to start of the blog series: Interpretable ML
Type 2 : Model Agnostic Interpretation (Continued)
| Interpretablility | Accuracy | |
| Complex Models | No | Yes |
| Simple Models | Yes | No |
-
Shapely Values
Lloyd Shapely, a Nobel Prize winner in 2012, came up with a cooperative game theory to distribute profits fairly. Basic premise is that if a group of people come together to play a cooperative game and win some money, how do we distribute this winnings fairly among the players? The individual players themselves interact differently to achieve the outcome and therefore how do we decide the contribution of each member to the collective objective fairly?
A prediction can be explained by assuming that each feature value of the instance is a “player” in a game where the prediction is the payout. Shapley values – a method from coalitional game theory – tells us how to fairly distribute the “payout” among the features.
Let us take the following example: We have a trained machine learning model to predict apartment prices. For a certain apartment it predicts €300,000 and you need to explain this prediction. The apartment has a size of 50 m^2, is located on the 2nd floor, has a park nearby and cats are banned. The average prediction for all apartments is €310,000. How much has each feature value contributed to the prediction compared to the average prediction?
The feature values
park-nearby,cat-banned,area-50andfloor-2ndworked together to achieve the prediction of €300,000. Our goal is to explain the difference between the actual prediction (€300,000) and the average prediction (€310,000): a difference of -€10,000.How do we calculate the Shapley value for one feature? The Shapley value is the average marginal contribution of a feature value across all possible coalitions. The following list shows all coalitions of feature values that are needed to determine the Shapley value for cat-banned. The first row shows the coalition without any feature values. The other rows show different coalitions with increasing coalition size, separated by “+”. All in all, the following coalitions are possible:
- No feature values
park-nearbysize-50floor-2ndpark-nearby+size-50park-nearby+floor-2ndsize-50+floor-2ndpark-nearby+size-50+floor-2nd
For each of these coalitions we compute the predicted apartment price with and without the feature value
cat-bannedand take the difference to get the marginal contribution. The Shapley value is the (weighted) average of marginal contributions. We replace the feature values of features that are not in a coalition with random feature values from the apartment dataset to get a prediction from the machine learning model.Accurate calculation of Shapely Values is a NP-Hard problem. Hence, we come up with a way of estimating it and one of the ways is SHAP.
-
SHAP (SHapley Additive exPlanations)
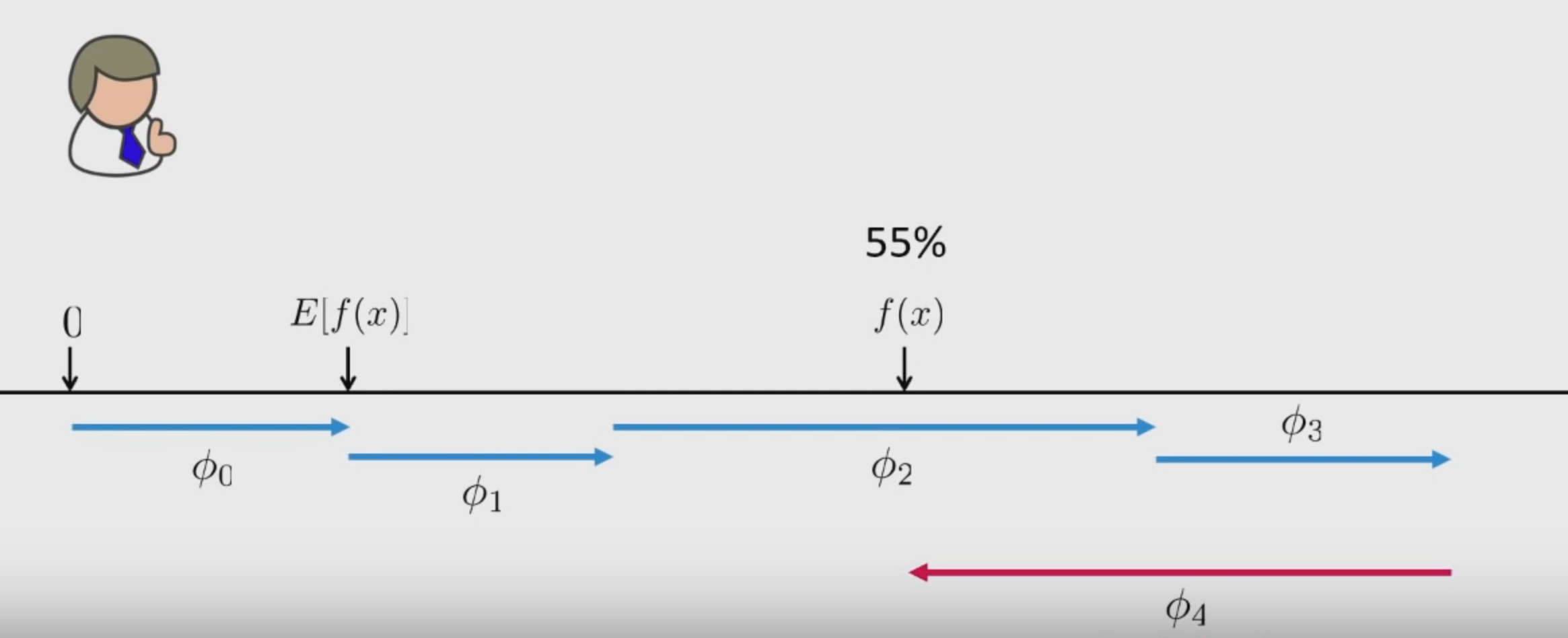
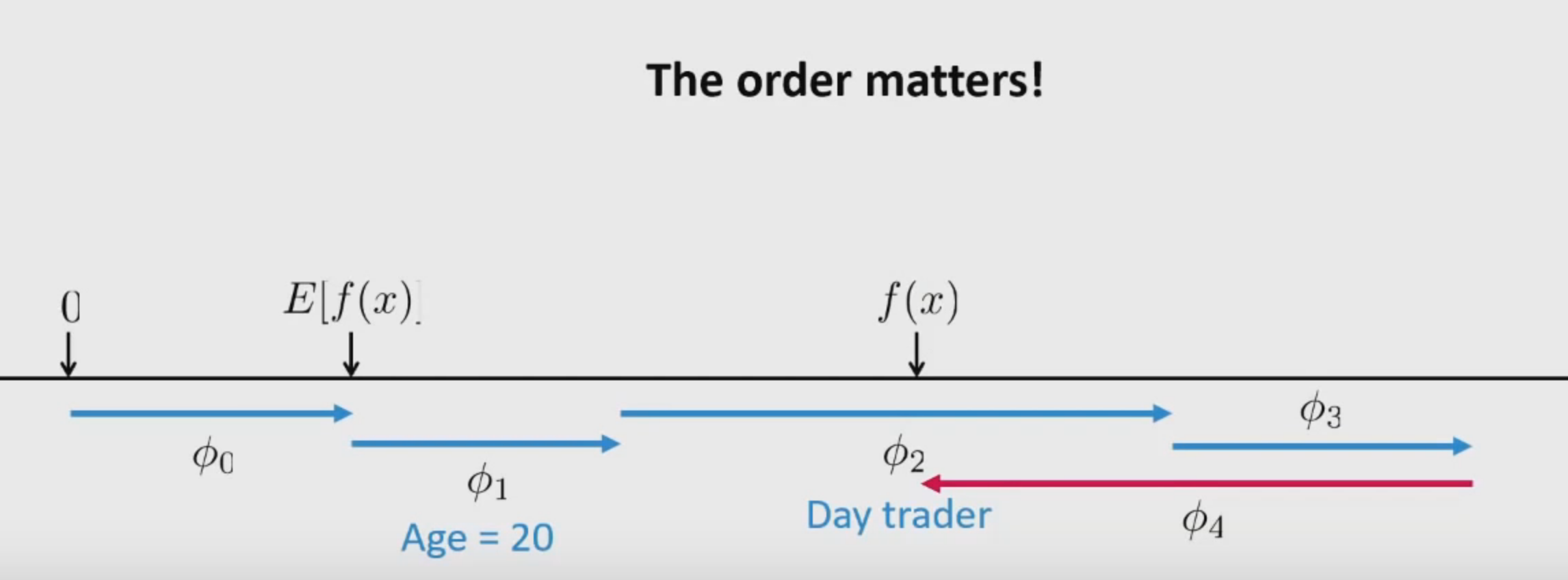
Here, \(\phi\) is the feature attribution function that estimates feature importance.
- Base Rate: Expectation of the model i.e mean of all predictions over the training data. \(E\left [ f(x) \right ]\)
- Change in rate given a feature \(x_{1}\):
- Change in rate given features \(x_{1}, x_{2}, x_{3}\):
The main assumption is that: \(x_{1}\), \(x_{2}\) and \(x_{3}\) are conditionally independent.
- Using LIME principles to estimate Shapely Values:
- LIME uses a local kernel with a loss minimization function (an exponentially smoothed kernel) with regularization. We have to pick a loss function, regularizer and a local kernel. If you remember, from the previous post on LIME, I stated that this is a point of weakness of LIME as they were chosen heuristically.
- LIME trains a linear model with the heuristic parameters. SHAP proposes that instead of using these heuristics, we can use Shapely Values (estimated through linear models) with a theoretical basis which obey the Shapely Principles.

An important thing to note here is that SHAP is not causal. It has scope for future work here. But, explainability is not causality i.e we are just explaining why a model gave a particular result without asserting that these features cause these outputs. A very important distinction.
- More information about SHAP can be found at this talk by Lundberg, the creator of SHAP.
- Link to the paper: A Unified Approach to Interpreting Model Predictions
- Github Source
