Hidden Markov Models (HMM): Theoretical Background

06 Dec 2017

Hidden Markov Models (HMM) were the mainstay of generative models a couple of years ago. Even though more sophisticated Deep Learning generative models have emerged, we cannot rule out the effectiveness of the humble HMM. After all, one of the most widely known principle (Occam’s Razor** states that if you have a number of competing hypothesis, the simplest one is the best one. The purpose of this blog post is to explore the mathematical basis on which HMMs are built.

Hidden Markov Models are characterized by two types of states, Hidden States and Observable States. Any HMM can be represented by three parameters:

Transition Probability:

The probability of the model to transition from one hidden state to the other given the current state.

Emission Probability:

The probability of the model to emit an observable state given the current hidden state.

Initial Probability:

The probability of the model being in a specific hidden state when it starts off.

Graphically, HMM are represented using a Trellis Diagram:

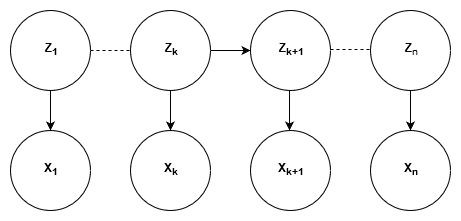
There are four algorithms fundamental to HMM: Forward algorithm, Backward algorithm, Forward-Backward algorithm and Viterbi Algorithm.

Forward Algorithm: Goal - To calculate \(P(Z_{k},X_{1:k})\)

Using marginalization,

\[\sum_{Z_{k-1}}^{n}P(Z_{k},Z_{k-1},X_{1:k})\] \[\sum_{Z_{k-1}}^{n}P(X_{k},X_{1:k-1},Z_{k},Z_{k-1})\] \[\sum_{Z_{k-1}}^{n}P(X_{k}|X_{1:k-1},Z_{k},Z_{k-1})P(Z_{k}|Z_{k-1},X_{1:k-1})P(Z_{k-1},X_{1:k-1})\]

Since \(X_{k}\), \(X_{1:k-1}\) and \(Z_{k-1}\) are independent,

\[\sum_{Z_{k-1}}^{n}P(X_{k}|Z_{k})P(Z_{k}|Z_{k-1})P(Z_{k-1},X_{1:k-1})\] \[\alpha_{k} = \sum_{Z_{k-1}=1}^{n}(Emission Probability)(Transition Probability)\alpha_{k-1}\]

Backward Algorithm: Goal - To calculate \(P(X_{k+1:n}\|Z_{k})\)

Using marginalization,

\[\sum_{Z_{k+1}=1}^{n}P(X_{k+1}, X_{k+2:n}, Z_{k+1}| Z_{k})\] \[\sum_{Z_{k+1}=1}^{n}P(X_{k+1}| X_{k+2:n}, Z_{k+1}, Z_{k})P(X_{k+2:n}| Z_{k+1}, Z_{k})P(Z_{k+1}| Z_{k})\] \[\sum_{Z_{k+1}=1}^{n}P(X_{k+1}| Z_{k+1})P(X_{k+2:n}| Z_{k+1})P(Z_{k+1}| Z_{k})\] \[\beta _{k} = \sum_{Z_{k+1}=1}^{n}(Emission Probability)\beta_{k+1}(Transition Probability)\]

Forward-Backward (Baum Welch) Algorithm: Goal - To calculate \(P(Z_{k}\|X)\) where \(X = (X_{1}, X_{2},.. X_{n})\) and \(P(Z_{k}|X)\propto P(Z_{k},X) = P(X_{k+1:n}|Z_{k},X_{1:k})P(Z_{k},X_{1:k})\)

Here, \(X_{k+1:n}\) is independent of \(X_{1:k}\) given \(Z_{k}\)

\[P(Z_{k},X) = P(X_{k+1:n}|Z_{k})P(Z_{k},X_{1:k})\] \[P(Z_{k},X) = (Backward Algorithm)(Forward Algorithm)\]