Sujay S Kumar

Masters in Intelligent Information Systems (MIIS)

School of Computer Science, Carnegie Mellon University

Acoustic Modeling (ASR Part 2)

05 Dec 2018

Link to the start of ASR series: Automatic Speech Recognition (ASR Part 0)

This blog post explores the acoustic modeling component of ASR systems.

Phonetics

Phonetics is the part of linguistics that focuses on the study of the sounds produced by human speech. It encompasses their production (through the human vocal apparatus), their acoustic properties, and perception. The atomic unit of speech sound is called a phoneme. Words are comprised of one or more phonemes in sequence. The acoustic realization of a phoneme is called a phone.

There are three basic branches of phonetics, all of which are relevant to automatic speech recognition.

Syllable

A syllable is a sequence of speech sounds, composed of a nucleus phone and optional initial and final phones. The nucleus is typically a vowel or syllabic consonant, and is the voiced sound that can be shouted or sung.

As an example, the English word \(\text{"bottle"}\) contains two syllables. The first syllable has three phones, which are \(b aa t\) in the Arpabet phonetic transcription code. The \(aa\) is the nucleus, the \(b\) is a voiced consonant initial phone, and the \(t\) is an unvoiced consonant final phone. The second syllable consists only of the syllabic cosonant \(l\).

Acoustic Modeling

Acoustic Model is a classifier which predicts the phonemes given audio input. Acoustic Model is a hybrid model which uses deep neural networks for frame level predictions and HMM to transform these into sequential predictions.

The three fundamental problems solved by HMMs:

Mathematical foundation to HMMs can be found in this post

Each phoneme will be modeled using a 3 state HMM (beginning, middle and end)

img

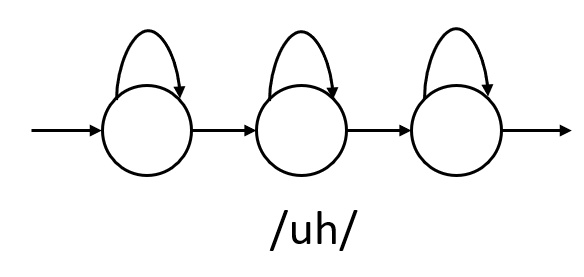
Word HMMs can be formed by concatenating its constituent phoneme HMMs. For example, the HMM word \(\text{"cup"}\) can be formed by concatenating the HMMs for its three phonemes.

img

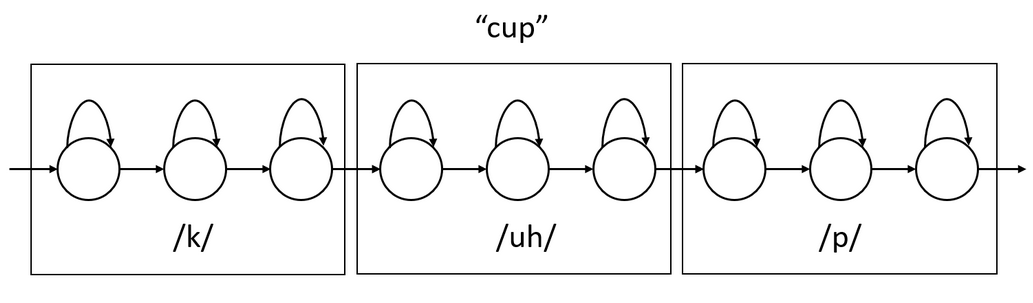
Therefore for training an Acoustic Model we need a word and its “spelling” in phonemes.

In HMM, each state has distribution over the observables (transition probabilities i.e a probability distribution over all the observable states from each hidden state). This distribution is modeled using a Guassian Mixture Models (GMM). There will be a separate GMM for each hidden state.

\[p(x|s) = \sum_{m}^{}w_{m}N(x;\mu_{m},\sum_{m})\]

where \(N(x;\mu_{m},\sum_{m})\) is Guassian Distribution and \(w_{m}\) is a mixture weight and \(\sum_{m}^{}w_{m} = 1\).

Thus, each state of the model has its own GMM. The Baum-Welch training algorithm estimated all the transition probabilities as well as the means, variances, and mixture weights of all GMMs.

Modern speech recognition systems no longer model the observations using a collection of Gaussian mixture models but rather a single deep neural network that has output labels that represent the state labels of all HMMs states of all phonemes. For example, if there were 40 phonemes and each has a 3-state HMM, the neural network would have \(40 \times 3 = 120\) output labels. Such acoustic models are called “hybrid” systems or DNN-HMM systems to reflect the fact that the observation probability estimation (transition probability) formerly done by GMMs is now done by a DNN, but that the rest of the HMM framework, in particular the HMM state topologies and transition probabilities, are still used. In simpler words, given an input MFCC vector, DNN will tell you what state it is in and of what phoneme. For eg, it might say that it is in the starting state of the phoneme \(/uh/\). Now, transitioning from this state to other state is handled by HMM.

Context Dependent Phones

In the previous section, we did context independent phones. For eg, for \(\text{"cup"}\), each phone \(/k/\), \(/uh/\), \(/p/\) were independent. In context dependent, each phone will have a preceding phoneme and succeeding phoneme which will be modeled. For eg, for \(\text{"cup"}\), HMM will look like this.

img

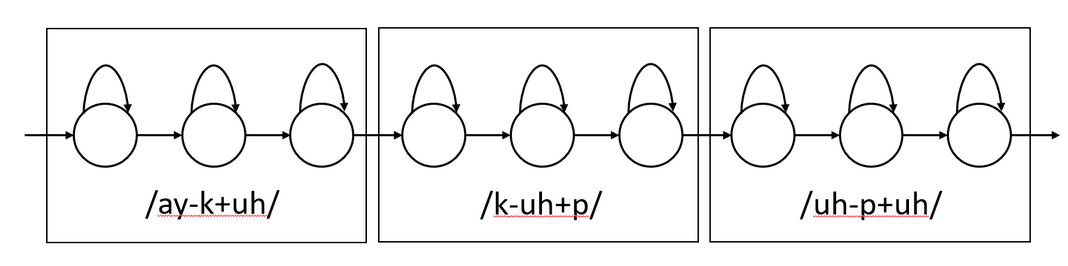
Because this choice of context-dependent phones models 3 consecutive phones, they are referred to as “triphones”. “quinphones” have a sequence of 5 consecutive phones.

In the previous example, we saw that since there were 40 phonemes and 3 states in each, we got 120 output labels. If we consider a triphone, number of phones will be \(40 \times 40 \times 40\) and 3 states each. Hence, we get 192,000 output labels.

This explosion of label space leads to 2 problems:

Solution to this problem is clustering. Cluster groups of triphones which are similar to each other into groups called “senones”. Grouping a set of context-dependent triphone states into a collection of senones is performed using a decision-tree clustering process. A decision tree is constructed for every state of every context-independent phone.

Steps to cluster:

  1. Merge all triphones with a common center phone from a particular state together to form the root node. For example, state 2 of all triphones of the form /-p+/.
  2. Grow the decision tree by asking a series of linguistic binary questions about the left or right context of the triphones. For example, “Is the left context phone a back vowel?” or “Is the right context phone voiced?”. At each node, choose the question with results in the largest increase in likelihood of the training data.
  3. Continue to grow the tree until the desired number of nodes are obtained or the likelihood increase of a further split is below a threshold.
  4. The leaves of this tree define the senones for this context-dependent phone state.

Doing this, reduces 192,000 triphones to about 10,000 senones. As you might have guessed, now we will be doing classification for senones instead of phones/triphones. Therefore, there will be a GMM for each senone. In hybrid, since we are replacing the GMM with DNN, there will be \((\text{number_of_senones} \times 3)\) output labels.

Sequence Based Objective Functions

In frame-based cross entropy, any incorrect class is penalized equally, even if that incorrect class would never be proposed in decoding due to HMM state topology or the language model. With sequence training, the competitors to the correct class are determined by performing a decoding of the training data.

Summary

So now we have a feed forward neural network that predicts which phoneme and which state. This is still frame independent i.e this is done for each frame. But in order to make it accurate, we append the previous frames and future frames to the current frame and give it as input.

Instead of this, we can as well train an RNN (with LSTM, GRU or a BiLSTM) which takes each frame in each time step and gives a prediction. But still, this is a frame independent procedure. (As an aside note, we need senone labels for each frame to train this network. That is generated by forced alignment. For forced alignment, we need an already trained speech recognizer to do the HMM decoding stage).

There is a disadvantage to this frame independent prediction. In cross entropy, we penalize all wrong classes equally. But for one target senone, there will be a set of commonly confused senones which have to be penalized more than others. This is where sequence objective functions come into picture instead of standard cross entropy.

Related Posts